Modeling Nature

Home > Data Modeling > Introducing Distribution

Introducing Distribution

Lesson 1B: Measuring Height

Preparing for the Lesson / Lesson Activities / Students' Ways of Thinking/ Assessment

Download documents

Prerequisites and Mathematical Concepts

Prerequisites

The activities in the lesson rest on a firm grasp of principles of measurement. Prior to the lesson, students should have opportunities to consider the nature of units of measure. For example, students could try to measure a distance in the classroom (or outside) using whatever tools they invent (but not standard tools, like a ruler). Activities like these help students consider the nature of units and how units are accumulated for measure. The theory of measurement progress map in the Assessment System describes these conceptual attainments in greater detail.

Mathematical Concepts

Students investigate variability by designing displays of trends that they notice in a collection of their measurements of the height of the flagpole. Comparison of different displays supports the development of meta-representational competence, meaning that students are encouraged to understand how every representation highlights some features of the data and backgrounds other features. Hence, representations are trade-offs. This quality of trade-off is a characteristic of all mathematical systems. We aim to help students better understand mathematical representation.

Top

Overview of the lesson

Students measure the height of an object, such as the school's flagpole or a tall tree, using indirect methods that involve triangle trigonometry. ( Triangle Investigations explores properties of triangles and triangle trigonometry, but the lesson can be conducted without this background.) To measure the height of the flagpole, students walk away from the base of the flagpole, stopping when their angle-measuring instrument indicates that their line of sight toward the top of the flagpole measures 45 degrees (implying that the angle between the top of the flagpole and the line of sight is also 45 degrees) . They then measure their distance from the flagpole base (B), which will be approximately the same (within measurement error) as a part of the height of the flagpole (A).

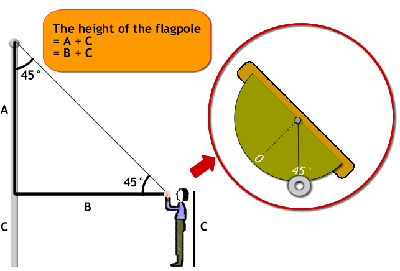
To correct for the fact that the 45-degree angle has been recorded at their eye level, they will need to add their own height (C) onto the estimated height of the flagpole (B), as illustrated in the diagram.

After each person has measured the height (at least once), the measures obtained are collected. Students work in small groups to design a display that shows, without words, all of the data and any of the trends about the data that they notice. Students post their displays and classmates, but not the designer, attempt to interpret their meaning. The pedagogical intention is to explore different senses of the �shape of the data. Student inventions are often idiosyncratic but the variability of student designs is important for grounding discussion about qualities of data display. Hence, the teacher employs a language for fostering meta-representational competence by asking the class to consider which features of the data are highlighted by a particular display and which it makes less obvious or even hides. The pedagogical intention is to foster the development of meta-representational competence. After discussing qualities of displays, the lesson concludes by soliciting students' ideas about sources of these qualities. What about the measurement process might lead to the shapes of the data observed?

Top