Although the entire lesson is intended as an assessment of the collective, teachers have elaborated on the lesson to get a better fix on student reasoning. Here we note some of the tasks and situations they developed to assess student reasoning and to support its development.

• ENACTMENT OF MEASUREMENT.
  Some teachers have found that asking students to measure something, such as the length of a line on the board, with a variety of tools including, but not only, rulers, is a good context for seeing what students attend to. Classroom conversations about different approaches or strategies are helpful for hearing how students talk about linear measure. Other approaches have included asking one student to measure the length from fingertip to fingertip of the outstretched arms of another students with a plastic water bottle. Many students think this is not possible, others begin measuring with the bottle in unexpected ways.

• OBJECT-ATTRIBUTE DISTINCTION.
  Some teachers have brought in a pile of dirt and asked students to list different qualities of that dirt that could be measured. Students have mentioned things like height, amount, weight, texture, and color. Other teachers have asked students if speed and distance are any different, and if so, how? (In one 6 th grade class, a student proposed that the difference was that speed involved "moving distances" and gave an example of a distance being moved during a longer and shorter interval of time).
  
• HOME-SCHOOL CONNECTIONS.
  Some teachers have found it helpful to ask students to list measurements they have seen or done outside of school. In school, they associate measurement with rulers. Outside of school, they seem to be more willing to consider other tools (like measuring cups and spring scales) and attributes other than length.

When teachers have tried this lesson, students often display patterns of thinking. We summarize some of the most salient patterns here:     

<Students' ways of thinking about measurement>

When students are asked what it means to measure something, students often think primarily of one attribute for every object. We hope that they come to think of an object as a bundle of potential attributes. For example, many students think that “measure” means to measure length: how long, how wide, or how tall.

When students are asked to give 3 really different examples of things they can measure and are asked why they think the 3 examples are different, students often tend to give examples of objects all with the same attribute. Here are some examples of students' thinking.

• Example 1: Pencil, book, eraser (They are different. They all aren't the same size.)
  
• Example 2: Your foot, a desk, and a note book ( Because one can be bigger and also they are different measure and they are not the same object.)
  
• Example 3: You can measure how much water is in a cup, how wide something is, or how big a cube is. (When you measure water, you use a measuring glass, when you measure how wide something is you just measure across the shape.)

Example 1 and example 2 illustrate that students interpret “really different examples of things” in terms of objects, not in terms of attributes that can be measured. Example 3 is illustrating more sophisticating idea that a student differentiates different attributes that can be measured and different tools to measure the attributes. [Object-attribute distinction]

.........................................................................................

When students are asked how they measure how long something is/ how heavy something is, and what are some important things to keep in mind, students often think of measurement as a set of procedures, without referencing the conceptual distinctions in measure (the big ideas). So, they might recall starting at 0 and to “use the marks” and to “read the number.”

Here are some examples of students' response.

• Example 1: With a ruler, yardstick, and rope. To always start at the 0 of a ruler
• Example 2: I would use a ruler to measure how long something is. I would keep in mind what the small marks mean on the ruler.
• Example 3: I would measure how heavy something with a scale. I would keep in mind that if the scale has a .5 that means half.
• Example 4: With a scale, If you aren't using a digital scale make sure it is on the zero.

Students named a ruler, yardstick, and rope as tools to measure how long something is. And for tools to measure how heavy something is, students said they would use a scale. Students responded that they would keep in mind that they always started at the 0 of a ruler or a scale. This suggests that students had some tacit knowledge of the importance of the origin of the scale, but students did not think that any number could serve as the zero-point.

<Students' ways of thinking about zero point>

The item below was asked to students to learn how students thought about the zero-point. Of the 21 students in a 6 th grade classroom, 6 students answered correctly. And six students answered the piece of wood was 3 ½ inches. It seems that those students who said the length of the piece of wood was 3 ½ just read the numbers on the ruler without thinking about the distance covered by the piece of wood.

Q: How long is the piece of wood?

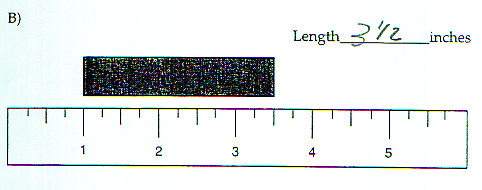
Here is another example that students think measurement as counting rather than as assigning numbers to magnitudes. In the video clip, one student is stretching out his two arms, and the other student is measuring the length of the outstretched arms from fingertip to fingertip with a plastic water bottle. Please notice that one student counts “One” with the movement of the water bottle.