Bai, Yiku; Tran, Huy; Damelin, Steven B.; Kolouri, Soheil. “Partial transport for point-cloud registration.” Sampling Theory, Signal Processing, and Data Analysis, vol. 23, no. 1, 2025, 4, https://doi.org/10.1007/s43670-025-00097-1.
Point cloud registration is a key task in areas like robotics, computer graphics, and medical imaging, where it’s necessary to figure out how different sets of points in 3D space relate to each other. However, challenges like irregular movements, parts of the object being hidden, or sensor errors make the task particularly tricky. Traditional methods can be slow, unreliable, and lack solid theoretical backing. Recently, the problem of point cloud registration has been approached using a technique called optimal transport, which includes variations like the optimal partial transport problem. These methods treat point clouds as sets of data and provide a solid mathematical approach to determine how the points in one set match up with another after transformation.
In this paper, we focus on solving the point cloud registration problem using optimal transport theory and introduce new methods for non-rigid registration based on the optimal partial transport problem. We also improve computational efficiency by using a simplified solution to a related problem and extending it to handle more complex cases, resulting in faster and more reliable registration algorithms. To show how well our methods work, we test them against traditional approaches on various 3D and 2D registration problems that involve noisy data.
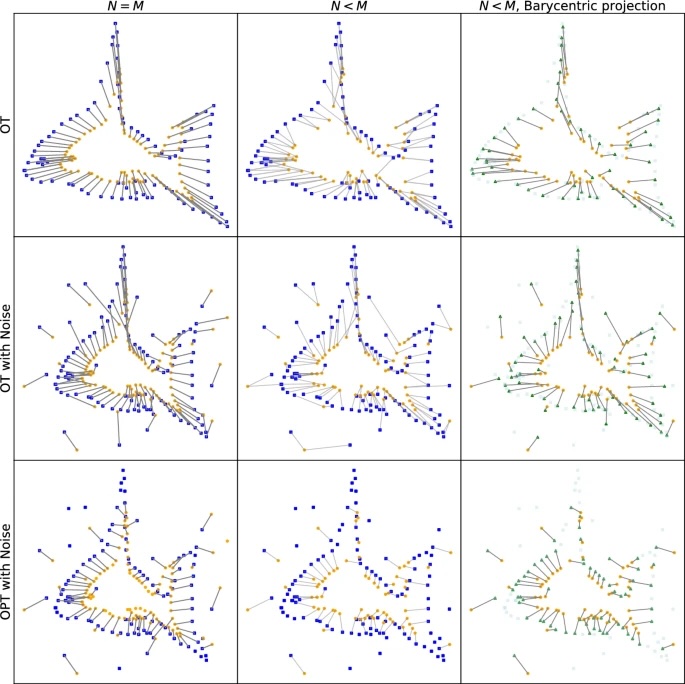
Fig 1
In the first column , the optimal transportation plan provides a hard assignment where every point has at most one correspondence. In the second column , the optimal transportation plan induces a soft assignment, which can be turned into a hard assignment with the barycentric projection of , as shown in the third column