Kolouri, S., Naderializadeh, N., Rohde, G. K., & Hoffmann, H. (2021). WASSERSTEIN EMBEDDING FOR GRAPH LEARNING. ICLR 2021 – 9th International Conference on Learning Representations, 34. https://www.scopus.com/inward/record.uri?eid=2-s2.0-85150286096&partnerID=40&md5=8b88e110167be2c5fd01da171324d3d6
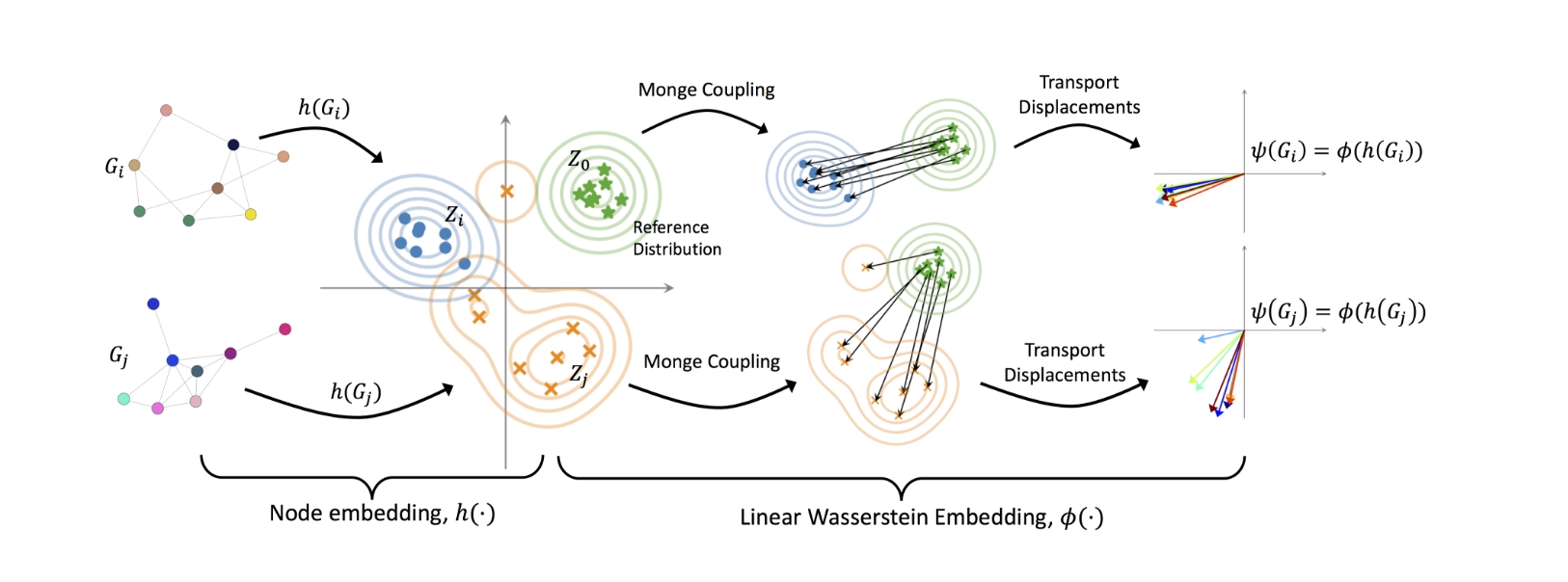
We introduce a new method called Wasserstein Embedding for Graph Learning (WEGL), which is a fast and efficient way to turn entire graphs into a form that can be used by machine learning models. Graphs are made up of nodes (points) and edges (connections), and we want to find a way to compare graphs to make predictions based on them. Instead of comparing every pair of nodes in different graphs, WEGL looks at the overall patterns of the nodes in each graph. It uses a special method called the Wasserstein distance to measure how different these patterns are between graphs. This approach is much faster than older methods, which required comparing every single node in one graph to every node in another graph. We also use a process called Monge maps to transform each graph into a simple, fixed-size vector (a list of numbers) that can be easily used by machine learning models. This makes it much easier to work with graphs for prediction tasks, like figuring out their properties. When we tested this method on various tasks, it performed very well, providing top-notch results while being more efficient than previous methods. The code to use WEGL is available at https://github.com/navid-naderi/WEGL.