Li, M.; Schilling, K.G.; Xu, L.; Choi, S.; Gao, Y.; Zu, Z.; Anderson, A.W.; Ding, Z.; Gore, J.C. “White matter engagement in brain networks assessed by integration of functional and structural connectivity.” NeuroImage, Volume 302, 2024, Article 120887, DOI: 10.1016/j.neuroimage.2024.120887.
Brain network models can be enhanced by combining structural data from white matter (via diffusion MRI) with functional data from gray matter (via resting-state BOLD signals). Diffusion MRI shows how white matter tracts connect gray matter regions, and we developed a method to assess how each white matter voxel contributes to brain function by integrating these connections. This creates detailed maps of white matter engagement, identifying areas critical for brain communication. These maps are highly consistent across individuals and highlight how gray matter activity depends on white matter organization. We also observed that white matter engagement varies over time and differs between genders, indicating its potential as a tool for understanding brain function and identifying neurological disorders.
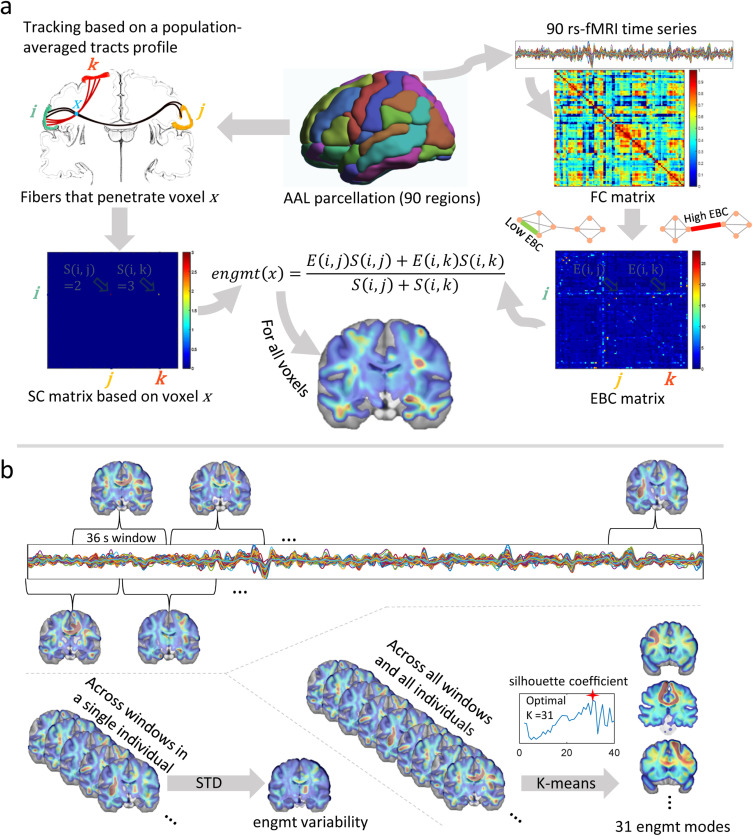
Fig. 1. Reconstruction and Analysis of Dynamic White Matter Engagement.
1a: Workflow of WM engagement reconstruction. The brain is parcellated into 90 GM regions using the AAL atlas. Following the left path, fiber tracking is performed considering each WM voxel x as a seed point. This tracking process retrieves all fibers that transverse x and connects to different pairs of GM regions. This created a 90×90 SC matrix, in which each element S(i,j) indicates the number of fibers connecting regions iand j and pass through x. Following the right path, FC is calculated based on the fMRI time series of the 90 regions, producing an FC matrix based on Pearson’s correlation coefficients. Using graph theory, a 90×90 EBC matrix is calculated where each element E(i,j) represents the functional importance of the connection between i and j. Voxel engagement (engmt) of x is then computed as a weighted average of the EBC elements, with the SC values serving as weights.
1b: Dynamic Engagement Analysis. To capture the temporal dynamics of voxel engagement, the time course is divided into overlapping windows of 36 seconds. The standard deviation (STD) of voxel engagement across these windows quantifies temporal variability. The clustering of concatenated engagement maps from all windows and subjects via k-means results in 31 mode maps, each representing a cluster center. The silhouette coefficient method determines the optimal number of clusters. Mode occurrence is measured by the frequency of each mode map across the time course for each subject, reflecting the dynamic engagement of voxels in the network.