Tran, Huy, Bai, Yikun, Kothapalli, Abihith, Shahbazi, Ashkan, Liu, Xinran, Martin, Rocio Diaz, & Kolouri, Soheil. (2024). Stereographic spherical sliced Wasserstein distances. In Proceedings of the 41st International Conference on Machine Learning (ICML 2024), Vienna, Austria, July 21-27, 2024, Volume 235, Pages 48494-48564.
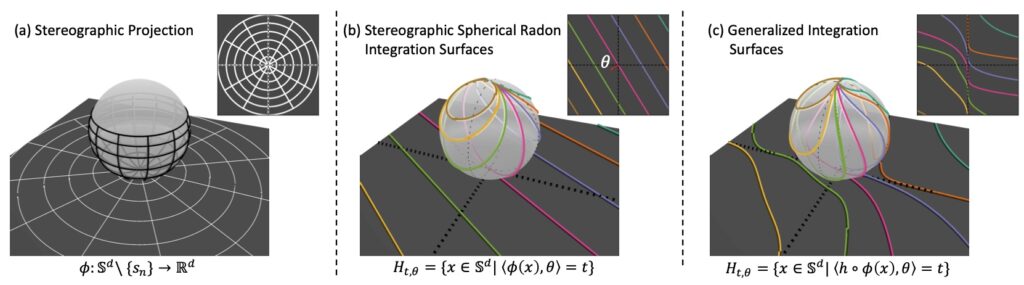
This study presents a new method for comparing spherical probability distributions, which are important in fields like geology, medical imaging, computer vision, and machine learning. Traditional methods, such as the Wasserstein distance, are often used to measure differences between probability distributions, but calculating these distances on spherical surfaces can be computationally challenging. To address this, the authors introduce the Stereographic Spherical Sliced Wasserstein (S3W) distance, a high-speed and parallelizable approach that leverages stereographic projection and the generalized Radon transform to efficiently compute distances between spherical distributions.
The authors tackle the issue of distortion caused by stereographic projection, ensuring the method remains accurate. They also analyze their metric in detail, providing both a theoretical framework and a rotationally invariant variation to account for the spherical nature of the data. Through a series of numerical experiments, including applications in gradient flows and self-supervised learning, they demonstrate that the S3W distance outperforms existing methods in both speed and accuracy.
This new distance metric offers a significant improvement for comparing spherical distributions, making it a valuable tool for researchers working in areas where spherical data is common. Additionally, the code for this method is freely available, allowing others to implement and build upon this work.