Nancy R. Newlin, Michael E. Kim, Praitayini Kanakaraj, Tianyuan Yao, Timothy Hohman, Kimberly R. Pechman, Lori L. Beason-Held, Susan M. Resnick, Derek Archer, Angela Jefferson, Bennett A. Landman, and Daniel Moyer. “MidRISH: Unbiased Harmonization of Rotationally Invariant Harmonics of the Diffusion Signal.” Magnetic Resonance Imaging, 2024, doi:10.1016/j.mri.2024.03.033.
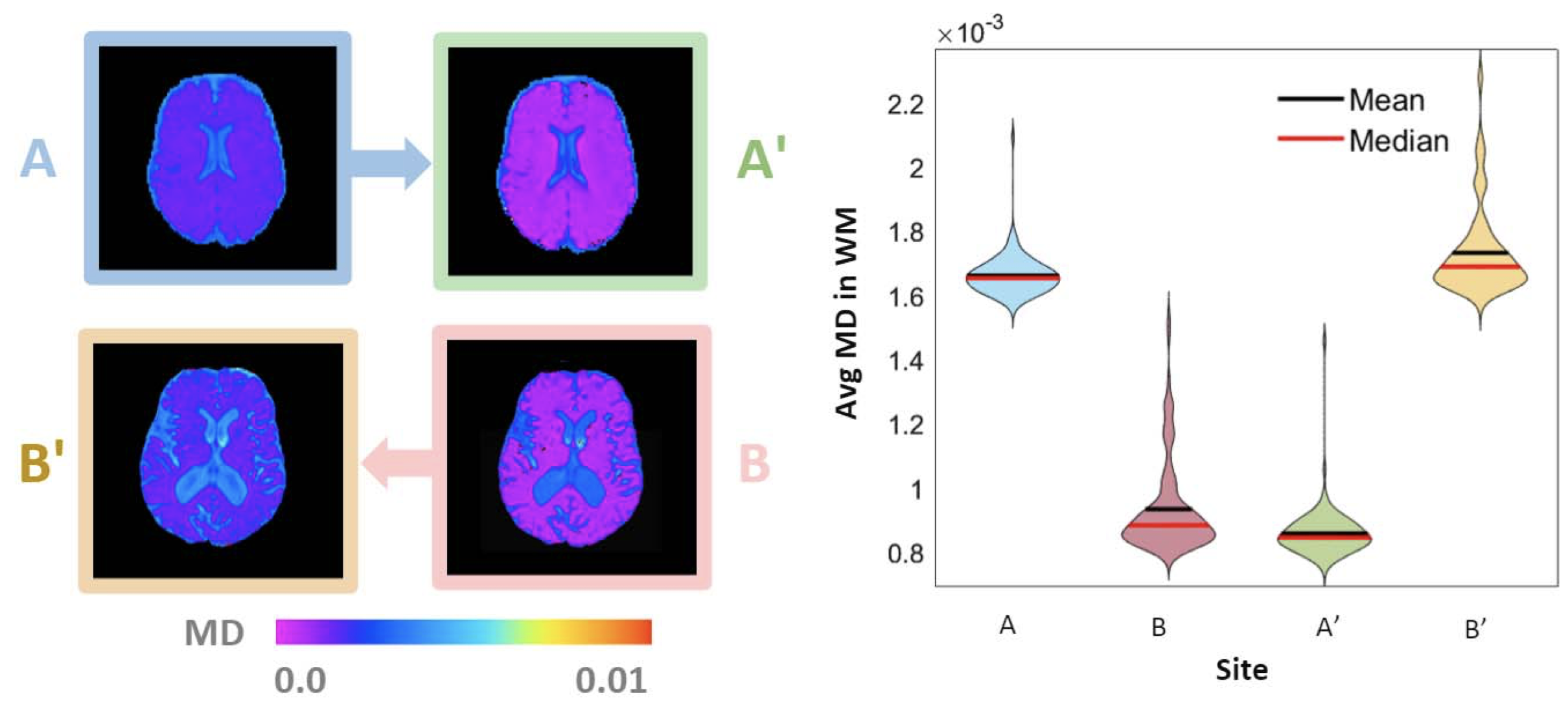
Data harmonization is essential for eliminating confounding effects in multi-site diffusion image analysis. One such harmonization method, LinearRISH, scales rotationally invariant spherical harmonic (RISH) features from a “target” site to match those from a “reference” site, aiming to reduce scanner-related confounding effects. However, the designation of reference and target sites is not arbitrary, and this choice can bias the resulting diffusion metrics such as fractional anisotropy and mean diffusivity. This study introduces MidRISH, a method that projects both sites to a mid-space, thereby avoiding the bias introduced by reference site selection. The MidRISH method was validated through two experiments: harmonizing scanner differences in 37 matched patients free of cognitive impairment, and harmonizing acquisition and study differences in 117 matched patients free of cognitive impairment. The results demonstrate that MidRISH reduces the bias associated with reference site selection while maintaining the harmonization efficacy of LinearRISH. Users should be cautious when using LinearRISH harmonization, as choosing a reference site impacts the effect size of diffusion metrics. The proposed MidRISH method eliminates the bias-inducing site selection step, offering a more robust approach to harmonization.